nLab loop braid group
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
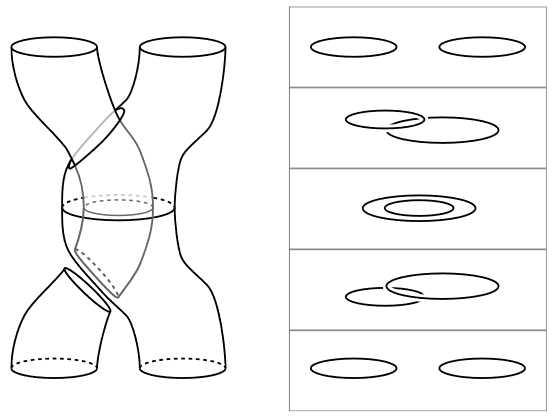
Idea
Where the braid group is the group of continuous “motions” of sets of distinct points in the Euclidean plane, the loop braid group (Dahm 62, Goldsmith 81) is the group of continuous motions of disjoint unknotted loops in 3d Euclidean space.
Accordingly, the role that the braid group plays in 3d TQFTs such as Chern-Simons theory/Reshetikhin-Turaev theory with point-like defects (anyons), the loop braid group plays in 4d TQFT with line defects (codimension-2 defect branes).
Related concepts
References
Original articles on motion groups:
-
D. Dahm, A generalization of braid theory, PhD thesis, Princeton University (1962)
-
Deborah L. Goldsmith: The theory of motion groups, Michigan Math. J. 28 1 (1981) 3-17 [doi:10.1307/mmj/1029002454]
Specifically on the loop braid group:
-
Deborah L. Goldsmith: Motion of Links in the 3-Sphere, Mathematica Scandinavica 50 2 (1982) 167-205 [jstor:24491407]
-
Xiao-Song Lin, The motion group of the unlink and its representations, in:
Xiao-Song Lin’s Unpublished Papers (doi:10.1142/9789812819116_others01), Part B of:
Kevin Lin, Zhenghan Wang, Weiping Zhang (eds.) Topology and Physics: Proceedings of the Nankai International Conference in Memory of Xiao-Song Lin, Tianjin, China, 27-31 July 2007. World Scientific, 2008 (doi:10.1142/6907)
-
Celeste Damiani, A journey through loop braid groups, Expositiones Mathematicae 35 3 (2017) 252-285 [doi:10.1016/j.exmath.2016.12.003]
-
Fiona Torzewska, João Faria Martins, Paul Purdon Martin, Motion groupoids and mapping class groupoids, Comm. Math. Phys. 402 (2023) 1621-1705 [arXiv:2103.10377, doi:10.1007/s00220-023-04755-0]
Monograph:
- Seiichi Kamada: Braid and Knot Theory in Dimension Four, Mathematical Surveys and Monographs 95, AMS (2002) [ISBN:978-0-8218-2969-1]
See also:
- Wikipedia, Loop braid group
Discussion via 4d TQFT and higher gauge theory/higher parallel transport:
in 4d BF-theory:
-
John Baez, Derek Wise, Alissa Crans, Exotic Statistics for Strings in 4d BF Theory, Adv. Theor. Math. Phys. 11:707-749, 2007 (arXiv:gr-qc/0603085)
-
Alex Bullivant, João Faria Martins, Paul Martin, Representations of the Loop Braid Group and Aharonov-Bohm like effects in discrete (3+1)-dimensional higher gauge theory, Advances in Theoretical and Mathematical Physics Volume 23 (2019) Number 7 (arXiv:1807.09551)
and in the 3d toric code-4d TQFT:
-
Liang Kong, Yin Tian, Zhi-Hao Zhang, Section 2.2 of: Defects in the 3-dimensional toric code model form a braided fusion 2-category, J. High Energ. Phys. 2020, 78 (2020) (arXiv:2009.06564, doi:10.1007/JHEP12(2020)078)
-
Zhen Bi, Yi-Zhuang You, Cenke Xu, Anyon and loop braiding statistics in field theories with a topological term, Phys. Rev. B 90 (2014) 081110(R) (doi:10.1103/PhysRevB.90.081110)
and in 3d symmetry protected topological phases:
-
Chao-Ming Jian, Xiao-Liang Qi, Layer Construction of 3D Topological States and String Braiding Statistics, Phys. Rev. X 4 (2014) 041043 doi:10.1103/PhysRevX.4.041043
-
Shenghan Jiang, Andrej Mesaros, and Ying Ran, Generalized Modular Transformations in (3+1)D Topologically Ordered Phases and Triple Linking Invariant of Loop Braiding, Phys. Rev. X 4 031048 (doi:10.1103/PhysRevX.4.031048)
and similar models in condensed matter theory:
-
Chenjie Wang, Michael Levin, Braiding Statistics of Loop Excitations in Three Dimensions, Phys. Rev. Lett. 113 (2014) 080403 (doi:10.1103/PhysRevLett.113.080403)
-
AtMa P. O. Chan, Peng Ye, Shinsei Ryu, Braiding with Borromean Rings in (3+1)-Dimensional Spacetime, Phys. Rev. Lett. 121, 061601 (2018) [arXiv:1703.01926]
-
Zhi-Feng Zhang, Qing-Rui Wang, Peng Ye, Wilson Operators, Non-Abelian Fusion Rules, and Loop Shrinking Rules of Borromean Rings Topological Order [arXiv:2208.09228]
Relation to braided tensor categories:
- Liang Chang, Representations of the loop braid groups from braided tensor categories, Journal of Mathematical Physics 61, 051702 (2020) (arXiv:2004.10896, doi:10.1063/5.0005266)
Relation to integrable systems:
- Pramod Padmanabhan, Abhishek Chowdhury, Loop braid groups and integrable models [arXiv:2210.12932]
Last revised on March 17, 2025 at 13:27:03. See the history of this page for a list of all contributions to it.